Feynman montre que certaines particules remontent le temps.
Hein???

Miam a écrit ::?: Où trouver une ombre des notions de statistiques et de probabilité chez Spinoza? Sans doute on remarque un développement des stats à partir du 17è siècle, chez Petty notament, mais il s'agit de statistiques sociales . Quant à la probabilité, il faudra attendre Hume: mais il s'agit là encore de degrés de clarté des idées
J'entend bien tes analogies et elles sont assez convaincantes sur la substance comme acte et l'unité des modes étendus et pensés qui empêche toute "présence" ontologique (la représentation de la chose comme présente est de l'ordre de l'imagination). Soit la position, soit la vitesse. Et un opérateur ontologique que nécessite la dépendance du système à l'observateur. Ne conviendrait-il pas de lier cette relativisation de l'objet à l'originalité de la conception du temps chez Spinoza. Feynman montre que certaines particules remontent le temps. Cela serait-il possible chez Spinoza. Et si oui, l'axiome cartésien "ce qui a été fait ne peut pas ne pas avoir été fait" demeure-t-il valide? Le temps spinozien n'est certainement pas newtonien (cad kantien).
Je ne perçois pas très bien l'opposition physique - mathématique. Un événement quantique est-il physique sans être mathématique ? Quel "préjugé" auraient, selon toi, les mathématiques ?
Je rappelle enfin que Stengers (qui parle de Withehead) est l'ancienne compagne de Prigogine, nobel belge de physique, qui a montré l'origine chaotique de la néguentropie dont sont issus de nouveaux systèmes thermodynamique, comme si le comportement aberrant, et comme "libre" de phénomènes locaux pouvaient produire de nouveaux systèmes stables. Stengers a peut être parfois trop creusé le côté "mystique" de cette "liberté" physique...
Miam a écrit ::?: "Une notion mathématique doit, logiquement, être dérivée d'un concept ontologique même si c'est à partir de la notion mathématique que nous est venu l'idée ontologique." Pourrais-tu préciser ?
Et puis en physique quantique, précisément, les opérateurs ontologiques ne sont ils pas des nécessités mathématiques ? Les mathématiques y sont-elles proches d'une ontologie générale, comme chez Descartes? Ou, comme chez Spinoza, bien qu'elles témoignent de la nécessité et de la certitude face au probabilisme scolastique (précisément), le nombre est il confiné à n'être qu'un auxiliaire de l'imagination? Préciser en ce sens.
Enfin: en quoi une particule qui remonte le temps contredirait-elle la conception spinoziste du temps?
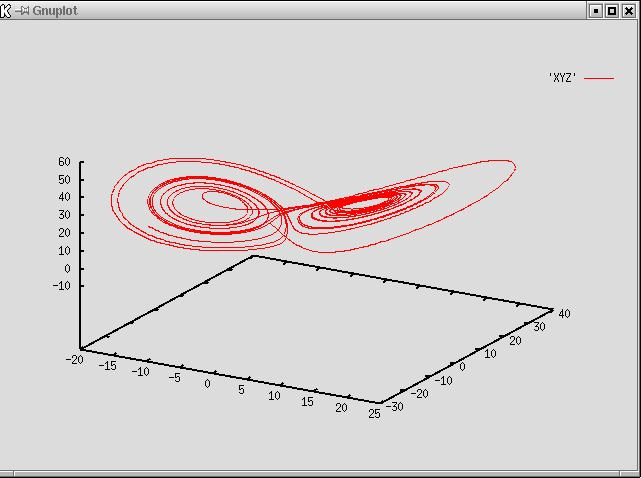 Ce peut être la représentation d'un être fini, d'un mode de l'être, une vie qui tourne autour d'un certain nombre de points clés, des attracteurs.
Ce peut être la représentation d'un être fini, d'un mode de l'être, une vie qui tourne autour d'un certain nombre de points clés, des attracteurs.

YvesMichaud a écrit :Si un phénomène était parfaitement cyclique, peut-on dire qu'il remonterait le temps?
Miam a écrit :(...) Je voudrais également demander à Bardamu ce qu’il en est du « formalisme » de cette physique quantique et, vu nos précédents messages, quelle est exactement la relation entre le concept et le nombre dans ce formalisme. Ce formalisme mathématique de Hilbert ou le formalisme logique post-frégéen reste-il toujours valide en physique quantique ? Et si non, précisément, qu’en est-il de son formalisme ?

Enfin, je voudrais faire remarquer qu’il serait quand-même fort étonnant que Spinoza puisse fonder la physique quantique quatre siècles à l’avance.
Aussi ne devrait-on pas prendre des exemples qui soient recevables par Spinoza ? Est-il loisible de prendre pour exemple la différentielle dans le passage (« transire ») à une plus grande (im)puissance alors que Spinoza ne connaissait pas encore le calcul infinitésimal ?
Le conatus est bien un « début ponctuel de mouvement » dès Hobbes, mais celui-ci l’allègue sans référence à l’infinitésimal. Dès lors, peut-on qualifier de « différentiel » les affects qui, cela dit et en effet, sont comme les délimitations modales de l’infinité propre au conatus et à la durée et dont la succession scande le développement d’une puissance indivisible et continue par elle-même ?Voilà. Y a du boulot!
Retourner vers « L'ontologie spinoziste »
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 1 invité